MATRIKS
1. Pengertian matriks
Matriks adalah susunan yang di atur menurut aturan
baris dan kolom dalam suatu jajaran berbentuk persegi atau persegi panjang. Bilangan-bilangan yang
terdapat pada suatu matriks disebut dengan elemen atau disebut juga anggota dari
suatu matriks. Contoh matriks dengan 2 baris dan 3 kolom yaitu sebagai berikut
:
Matriks banyak dimanfaatkan untuk menyelesaikan berbagai permasalahan
matematika misalnya dalam menemukan solusi masalah persamaan linear,
transformasi linear yakni bentuk umum dari fungsi linear contohnya rotasi dalam
3 dimensi. Matriks juga seperti variabel biasa, sehingga matrikspun dapat
dimanipulasi misalnya dikalikan, dijumlah, dikurangkan, serta didekomposisikan.
Menggunakan representasi matriks, perhitungan dapat dilakukan dengan lebih
terstruktur.
2. Macam-macam matriks
a. Berdasarkan banyak baris
dan kolom
1). Matriks baris
Yaitu matriks yang hanya
terdiri atas 1 baris. Ordo matriks yang terdiri atas 1 baris dan n kolom adalah
1 x n.
Contoh : A= ( 1 4 7 2 ) adalah matriks baris berordo 1 x 4.
2.) matriks kolom
Yaitu matriks yang hanya
terdiri atas 1 kolom. Ordo matriks yang terdiri atas m baris dan 1 kolom adalah
m x 1. contoh:
3). Matriks persegi panjang
Yaitu matriks yang
banyak barisnya tidak sama dengan banyak kolomnya. Matriks ini dapat di tulis
sebagai matriks berordo m x n. Contoh:
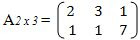
4). Matriks persegi
Yaitu matriks yang
mempunyai banyak baris dan kolom sama. Matriks persegi berordo n x n sering
disebut matriks persegi berordo n. Dalam matriks persegi, elemen-elemen yang
terletak pada garis hubung antara elemen a11 dan ann disebut
elemen diagonal utama, sedangkan elemen-elemen yang terletak pada garis hubung
antara elemen a1n dan an1 disebut elemen diagonal samping. contoh :
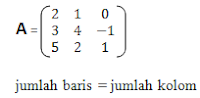
3.
Transpos suatu matriks
Yang dimaksud dengan Transpose dari suatu matriks adalah mengubah komponen-komponen dalam matriks, dari yang baris menjadi kolom, dan yang kolom di ubah menjadi baris.
Contoh:
Matriks
Contoh:
Matriks
-
- A =
ditranspose menjadi AT =
- A =
Matriks
-
- B =
ditranspose menjadi BT =
- B =
Rumus-rumus operasi Transpose sebagai berikut:
-
- 1.
- 2.
dan
- 3.
dimana k adalah skalar
- 4.
- 1.
4.
Determinan Suatu Matriks
Untuk menentukan determinan dari suatu matriks dapat digunakan beberapa cara :
1. Misalnya terdapat matriks  yang berordo 2×2 dalam menentukan determinan dari matrikas A yang biasa ditulis |A| adalah
yang berordo 2×2 dalam menentukan determinan dari matrikas A yang biasa ditulis |A| adalah
2. Metode Sarrus
Ubah matriks dalam bentuk seperti diatas selanjutnya perhitungannya dengan cara menambahkan elemen dari kiri atas kekanan bawah (mulai dari a → e → i, b → f → g, dan c → d → h) kemudian dikurangi dengan elemen dari kanan atas kekiri bawah (mulai dari c → e → g, a → f → h, dan b → d → i) maka akan menjadi
Sebagai contohnya
3. Metode Ekspansi Baris dan Kolom
Matriks Singular
Matriks Singular yaitu matriks yang nilai determinannya 0.
Sebagai contoh
Jika A matriks singular, tentukan nilai x!
Jawab:
Invers Matriks
Sifat-sifat dari invers suatu matriks :
Persamaan Matriks
Tentukan X matriks dari persamaan:
- Jika diketahui matriks A.X=B
- Jika diketahui matriks X.A=B
Contoh soal
1. Carilah matriks tranpose dari matriks berikut ini
Pembahasan :
Matriks tranpose A dari matriks A adalah
Matriks tranpose A dari matriks A adalah
2. Carilah matriks tranpose dari matriks berikut ini
Pembahasan :
Matriks tranpose A dari matriks A adalah
Matriks tranpose A dari matriks A adalah
5. Berapakah hasil kali matriks A.B dan B.A jika diketahui matriksnya adalah
a.

b.

Pembahasan :
a.

b.
6.Tentukan determinan dan invers dari matriks dibawah ini
a.

b.

Pembahasan :
a.cara mendapatkan determinan matriks A adalah
cara mendapatkan invers dari matriks A adalah
b.cara mendapatkan determinan matriks A adalah
cara mendapatkan invers dari matriks A adalah
-EKA SRI LESTARI-


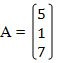



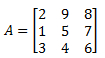


















Tidak ada komentar:
Posting Komentar